Game theory is the study of strategy from the perspective of mathematics. Recently, experimental economists have been studying the ability of human players to optimally play these games. In this section we shall study some basic concepts of game theory. Then we shall show how the Cournot- Stackelberg solutions of the duopoly problem from the previous section can be set up as a game. Then in a class period we will have a contest to see who can obtain the highest score playing this game repeatedly. There will be prizes for the highest three players.
The decision-makers in a game are caller players. While economists frequently study games with n players in this section we shall restrict our attention to games with only two players. The alternatives from which the players must choose are called strategies . In this section we shall restrict our attention to games with only two strategies, although we could easily consider any finite number.
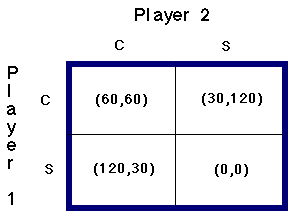
In this section we shall consider games in which each player chooses his or her strategy without knowing the other player's choice. The consequences or returns to each player when they both decide are called payoffs. A two by two game can be set up as a matrix. Let us consider a duopoly where if both firms play Cournot they both earn $60,000, which we will list as 60. Suppose one plays Cournot and the other plays Stackelberg. The Cournot player earns $30,000 (30) and the Stackelberg player earns $120,000 (120). If they both play Stackelberg then they both earn $0 (0). These choices can be organized as a matrix game.

The payoffs are shown in (xx, yy), where the first number is the payoff to Player 1 and the second number is the payoff to Player 2. For example, if Player 1 plays Cournot represented by C and Player 2 plays Stackelberg represented by S, Player 1 earns 30 and Player 2 earns 120. In the strategic pair, (C,S), the first element C is for the row player, Player 1 and the second element S is for the column player, Player 2 .
One important concept in game theory is the concept of a dominant strategy. A player has a dominant strategy if that strategy is superior independent of the other player's action. Another important concept is the concept of a Nash equilibrium: A pair of strategies (a*, b*) such that a* is an optimal strategy for Player 1 if Player 2 plays b*, and b* is an optimal strategy for Player 2 if Player 1 plays a*.
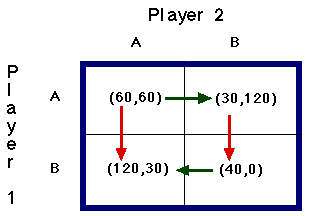
Arrow analysis of 2x2 matrix games: An easy way to analyze for dominant strategies and Nash equilibria is by drawing arrows as shown below.
Vertical arrows: Consider Player 2 with strategy C. If Player 1 plays C he or she receives 60, and if Player 1 plays S he or she receives 120. Since 120 is greater than 60, we draw a red arrow down from 60 to 120 indicating that 120 is greater. Now assume Player 2 plays S. Since 30 is greater than 0 we draw a red arrow up from 0 to 30.
Horizontal Arrows: Consider Player 1 with strategy A. Since 120 is greater than 60, we draw a green horizontal line from 60 to 120. Now consider Player 1 with strategy B. Since 30 is greater than 0, we draw a green horizontal line from 0 to 30.
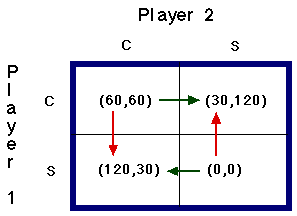
If you will examine the matrix above, neither player has a dominant strategy. There are two Nash equilibrium at (C, S) and (S, C). Another way to look at the concept of a Nash equilibrium is that at these corners neither player has an incentive to shift their strategies.
Now let us examine two more games with different payoffs:
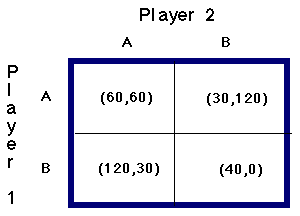
Game 1
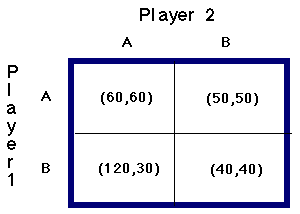
Game 2
For these two games we shall list the strategies as simply A and B for both players. Let us consider the arrow analysis of these two games:
Game 1
Game 2
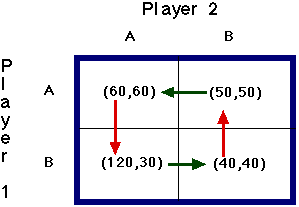
Arrow analysis:
Game 1: B is a dominant strategy for Player 1 because both red arrows point down. Player 2 does not have a dominant strategy because both green arrows point in opposite directions. (B, A) is a Nash equilibrium because the red and green arrows both point into this corner. None or the other strategy pairs in a Nash equilibrium.
Game 2: Neither player has a dominant strategy and there is no Nash equilibrium.
Repeated Games:
Suppose you and your opponent play the same game many times. To analysis the logic we start at the last period. Suppose you and your partner are playing the Cournot Stackelberg game 10 times and for 9 periods you and your partner have played (C, C). In the last period each of you will realize that to win you need to play S hoping your opponent will play C. Now let us reconsider your play in the 9th period. Since you know your partner is likely to break the implicit agreement in the last period, why not get the jump on your opponent and switch to S in the 9th period. If you consider the logic step by step back to the first period, you are likely to play S in the first period. This is the game we will play for prizes after Thanksgiving. Think about your strategy.
You can play this game by yourself. You should practice so that you will be ready when the class comes to the computer room to play for prize money. Click here to start.
To play the game the TA must start the server program on the same server that Netscape is running on. Once this program is operating, click here