The basis for the IS/LM model is that it presents the Keynesian system in a fashion such that economists trained in the thirties could understand the model. In the thirties economists did not study math and learned all economic arguments in the form of graphs. The reason I do not pursue graphs in this course is that this approach is obsolete. If you want pictures have your graphics package create them in color. If you look at the simple mathematical description of the IS/LM model you will note that it constitutes four equations in five unknowns. To reduce the model to four unknowns the price level p is taken as a known parameter, that is it is determined by economic forces not represented in the model. Since four equations can not be plotted on a two dimensional graph a device must be created to reduce the model to two equations.

The device used to reduce the 4 equation IS/LM model to two equations is to collapse all the equations dealing with fiscal policy, that is government spending and taxes into one equation -- the IS equation or investment savings. This equation contains the real side of the economy. The other equation is the LM equation which stands for Liquidity Money. Thus from a mathematical perspective the graphical treatment of the IS/LM model is picture approach to solving four equations in four unknowns. Because the setup parallels the picture analysis of supply and demand you might be correct in assuming this approach is loved by most economists and will be inflicted upon you like a plague in intermediate courses.

In your technical essay you might list the four equations in the IS/LM model. You do not need to memorize them as they are in the math section. List them in a neat package. Briefly explain each equation. List the IS equation which combines the three equations on the real side. This equation is listed in the math section. Explain what is going on -- that is a mathematical simplification for nonmath types. The IS/LM has now been reduced to:

_____ $$ Y = k(A - ci) IS _____ (1)

_____ $$ Ms/p = eY - fi LM ___ (2)

The symbols are explained in your Model II handout.

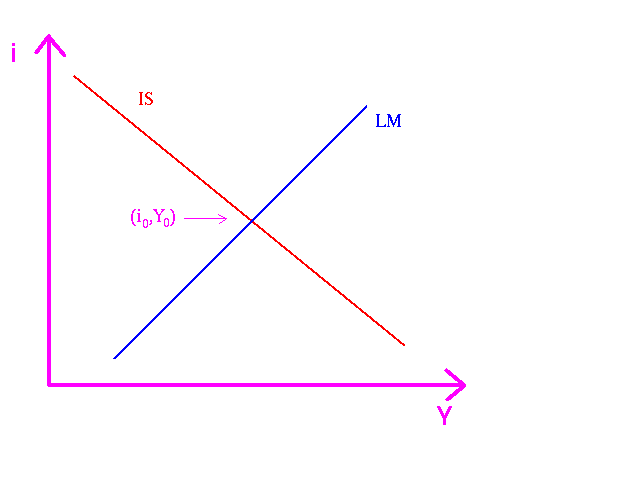
The graphical solution, the one you will see in intermediate courses, is as follows:

Thus the graph gives us the equilibrium $$Y and $$i. If we wished to find the equilibrium $$C we would substitute the equilibrium $$Y into the consumption function.

What this model is used for is to assess the effects of monetary, that is the effect of a change in $$Ms, and fiscal policy, the is a change in $$G or $$T. In the reduction of the model to two equations an important result was achieved. Changes in $$G or $$T affect only the IS equation and changes in Ms affect only LM equation. Thus for fiscal policy we have reduced everything to knowing whether the IS equation moves to the left or the right. Monetary policy is knowing whether the LM equation moves to the left or right. The model can also be used to study the effect of p, prices, on the equilibrium. Remember that this model does not determine prices. Prices are determined outside this model.

To remember how the equations are affected by movements in $$G, $$T, $$Ms, and $$p we need to reduce the number of variables to two. To do this remember that $$G and $$T are opposites and $$Ms and $$p are opposites. That is they have opposite effects. For example increasing $$G has the same effect as decreasing $$T. Fiscal policy is thus reduced to one item: Increasing G shifts the IS curve to the right. Why has fiscal policy been reduced to one item? Well if you have a logical mind you will realize that decreasing $$G shifts the IS curve to the left. Decreasing $$T shifts the IS curve to the right and so on. Likewise monetary policy can be reduced to one item. Increasing Ms shifts the LM curve to the right. The other three cases involving $$Ms and $$p logically follow. These results can be displayed in pretty, that is pretty for a 1930's economist, pictures:

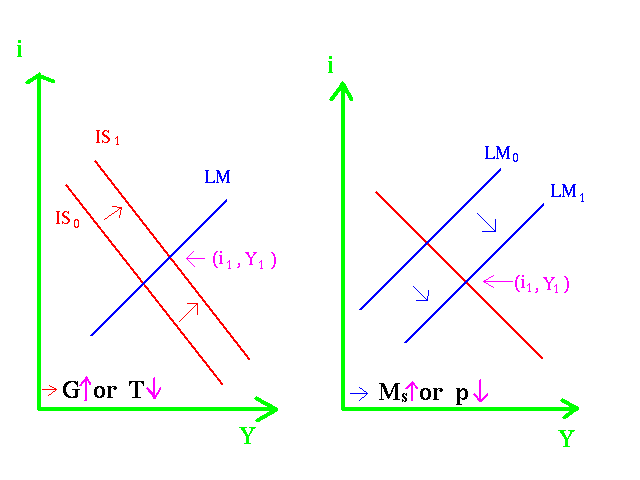
We note the if $$G increases $$Y increases but $$i also increases. If we examined the consequences on investment we would see a decrease in investment. This is one form of crowding out, that is increased government purchases crowded out private investment. This shows why fiscal policy must be coordinated with monetary policy. To keep $$i at the same level the FED could increase $$Ms shifting the LM curve to the right. This is called accommodation as shown below:

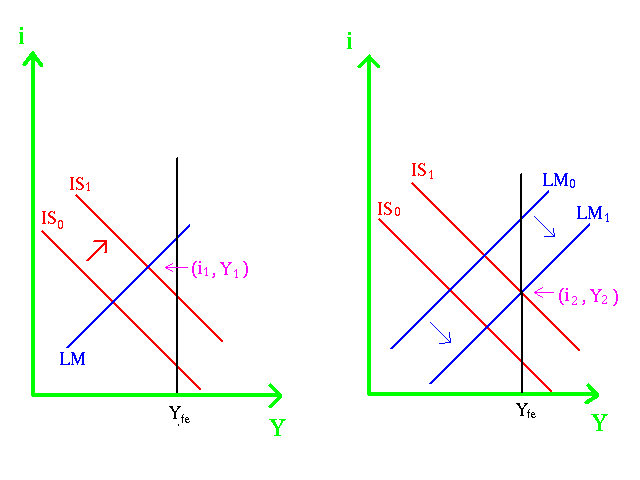
The fundamental problem with accommodation is that if this policy pushed $$Y beyond $$Y_fe then only inflation can occur. For full credit you should be able to give some policy prescriptions for various situations.

Previous

Index

Next