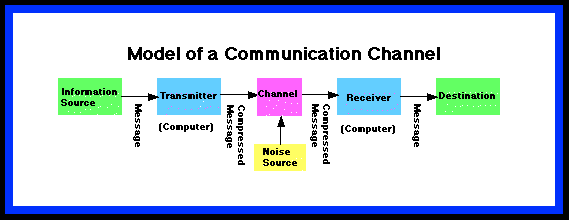
Shannon in 1949 developed a theory of communication based on a measure of information which enables communication engineers to determine the communication capacity required to communicate the messages. In order to discuss Shannon's measure of the information content in a message, consider the following simple diagram of a communication system:

At the information source the input message is digitized and at the destination the message is converted back into the input form, that is, text, voice, etc. Noise will cause the output to differ from the input. To build a communication system, we need know the volume of the message. Intuitively, consider a fresh water system in a city. To build this system you must know the size of pipe to transmit the desired amount of water to each household. Since we have converted the message into binary code, Shannon's contribution was to define the message volume in bits.
To gain some intuitive understanding of his concept we need to consider some examples. If you had to transmit an infinite string of 1's with no zero's, you can use the string's pattern to greatly compress the number of bits you must transmit. In this case, once you remove the pattern there is nothing left to transmit. Now suppose 0's were placed at random intervals in the string of 1's. You would have to transmit the pattern of all ones and also transmit the locations of the zero's. The greater difficulty in transmitting the second message over the first is directly related to the number of randomly spaced 0's. Now consider a picture composed of a green field. To transmit the message all you must transmit is the pattern. The video message becomes progressively more difficult to transmit depending on the number of blue dots randomly placed in the picture. The Shannon information message is a measure of the randomness, or entropy, of the message. Shannon's measure says nothing about the meaning of the message. The communication engineer does not care whether the message is nonsense syllables or national secrets. Entropy or randomness refers to number of bits required to transmit the random elements. Shannon is very important because he provided communication engineers with a theory for designing appropriately sized communication channels for transmitting the information content of the messages. If the channel capacity is greater than the information measure (entropy) of the message, it is theoretically possible to transmit the message without error in a noisy channel. On the crest and trough of every wave you can place a bit or no bit. Thus to transmit a message the frequency of channel must be greater than one half the number of bits which must be transmitted per second.