Math for Microeconomics

Introduction

In this section we shall present the basic math tool to solve one variable optimization problems. In this course math is a tool to solve economics problems.

Derivative

Function f: For any element

f(x) is an element in the range of

f corresponding to element

x in the domain. A function

f can be represented as a graph

{(x,y): y =f(x)} for all

x in the domain of

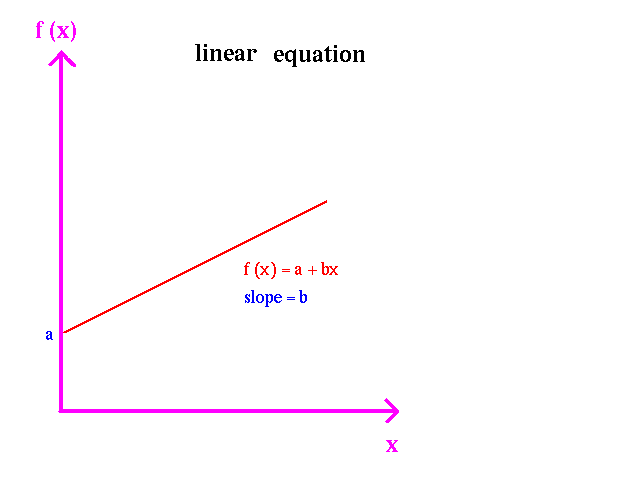
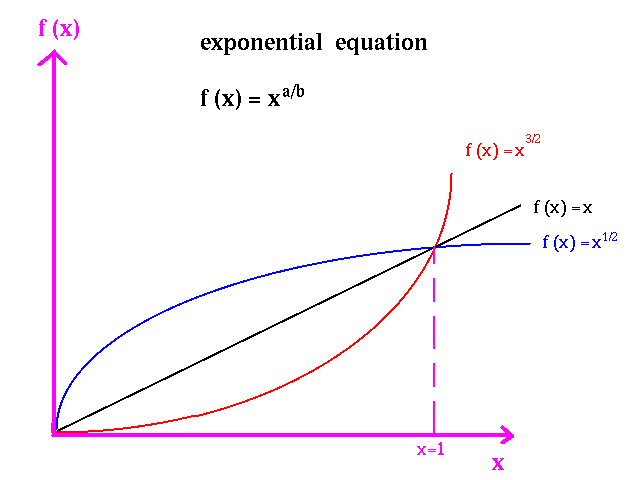
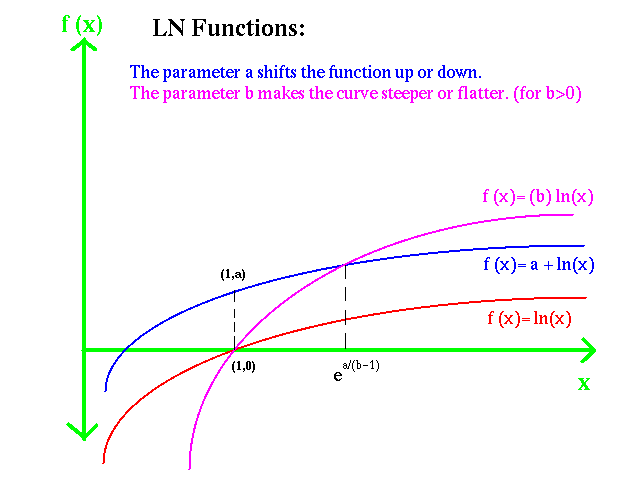
The most common functions used in Economics are linear functions, functions to fractional exponents, and ln functions.
Linear: f(x) = a + bx
Fractional exponent: f(x) = x^a/b
Ln f(x) = a + b ln(x)

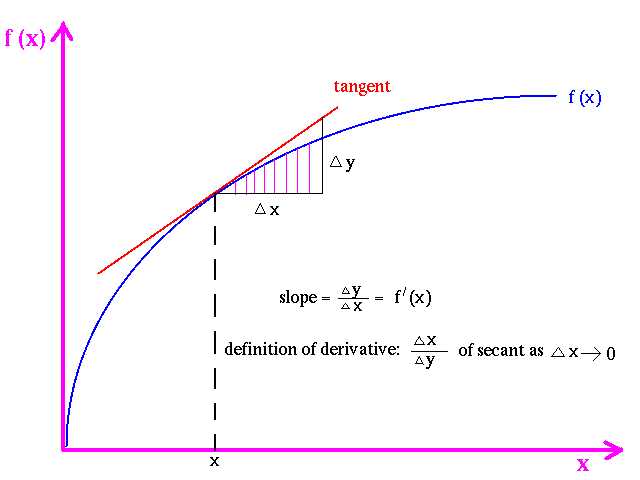
Derivative f'(x): The derivative of f at x, denoted as f'(x) or df/dx is defined as:
f'(x) = lim([f(x+h) - f(x)]/h) as h -> 0

The type of functions we will consider in this course will be differentiable at almost all points in their domains.

It is important to note that the derivative has a geometric interpretation. The derivative f'(x) is the slope of the tangent line to f at x.

In taking derivatives we could go back to first principles and use the definition to derive them. It is much easier to use the rules derived from the definitions.

Derivative Rules

1. f(x) = xⁿ f'(x) = n x^n-1

2. f(x) = x^a/b f'(x) = (a/b) x^(a/b)-1

3. f(x) = ln x f'(x) = 1/x<

Examples:
1. f(x) = x f'(x) = x⁰ = 1
2. f(x) = x⁴ f'(x) = 4x³
3. f(x) = x^2/3 f'(x) = (2/3)x^-(1/3) = 2/[3x^(1/3)]

There are three rules involving functions of functions which we will use repeatedly in the course.

1 Product Rule: Given functions g(x) and h(x) with f(x) = g(x)h(x):

f'(x) = g'(x)h(x) + g(x)h'(x)

2.Quotient Rule: Given functions

g(x) and

h(x) with

f(x) = g(x)/h(x):

f'(x) = [g'(x)h(x) - g(x)h'(x)]/[h(x)]²

3.Composite Function Rule: Given functions

g(x) and

y= h(x) with

f(x) = g(h(x)) = g(y) What this means is that for a given

x, y = h(x) is the input for

g( ) :

f'(x) = g'(y)h'(x)
We could also write it as:

df/dx = (dg/dy)(dy/dx).

Examples:

1. f(x) = ln (x²)
_ f'(x) = (1/x²)2x = 2/x

2. f(x) = g(x)h(x) = (x² - 3x)(2x³ - 1)
_ f'(x) = g'(x)h(x) + h'(x)g(x)
_____ = (2x - 3)(2x³ - 1) + (6x²)(x² - 3x)
_____ = 10x⁴ - 24x³ - 2x + 3

3. f(x) = (3x² + 2x + 1)²
_ f'(x) = 2(3x² + 2x + 1)(6x + 2)

4. f(x) = g(x)/h(x) = x²/(2x - 1)
_ f'(x) = (g'(x)h(x) - h'(x)g(x))/(h(x))²
_____ = (2x(2x - 1) - 2x²)/(2x - 1)²
_____ = (2x² - 2x)/(2x - 1)²

5. f(x) = g(x)/h(x) = (x² - 3)/x²
_ f'(x) = (g'(x)h(x) - h'(x)g(x))/(h(x))²
_____ = (2x(x²) - 2x(x² - 3))/(x²)² = 6/x³

6. f(x) = g(x)h(x) = 2x²(3x⁴ - 2)
_ f'(x) = g'(x)h(x) + h'(x)g(x) = 4x(3x⁴ - 2) + 2x²(12x³)
_____ = 36x⁵ - 8x

7. f(x) = 3 ln(x² - 1)³
_ f(x) = 3 ln(y);____ y = w³; ____w = x² - 1
_ f'(x) = (3/y)3w²(2x)
_____ = (3 [3(x² - 1)² (2x)]/(x² - 1)³
_____ = 18x/(x² - 1)

8. f(x) = (x² + 1)³(x³ - 1)²
__ f(x) = uv;____ u = w³; w = x² + 1; v = z²; z = x³ - 1.
_ f'(x) = v (3w²2x) + u(2z3x²)
_____ = 6(x³ - 1)²(x² + 1)²x + 6(x² + 1)³(x³ - 1)x²

Quiz

Index